AtCoder青 / CodeForces紫になりました
はじめに
この記事はdokinさんが作成した「色変記事 Advent Calendar 2020」 14日目の記事です。
前日はMdさんの「AtCoder黄色になりました」,翌日はもすーんさんの「AtCoder青色になりました!(もうダメです)」です。
(AtCoderのレート/CodeForcesのレートが)
AtCoder青 / CodeForces紫になりました!!!!
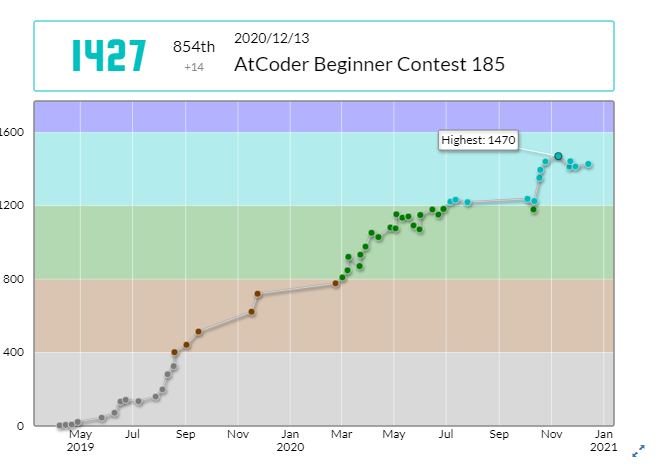

$\dfrac{1427}{1719}≒\dfrac{1600}{1928}$らしいです。
おまけ
よくよく見ると2つのグラフは同じような概形をしていることが分かります。
コンテスト時のメンタルが前回の結果に影響されているみたいですね。一方で,自分の実力が中途半端ということもあって「力こそPower」といったゴリ押しはできずその場で取った戦略次第でコンテストの成績が決まってしまう(リカバリーが苦手で他の人が普通に解けるところでずっと詰まっていたことも...)。ということが多かった気がします。
よって,年内の色変の為にできることは次の2つがあげられるのではないでしょうか。
- 複数のコンテストで固定した戦略をあらかじめ立てておく(日々のバチャでその戦略を練習しておく)
- 典型埋めを行う
- (非本質な点で時間やメンタルを喰わないように,環境を整えておく)
これ以上書けることもないので今回の記事はこのあたりで締めることにします。今後(できれば年内に)色変が達成できた場合,また別の記事を書こうと思うので,今後もよろしくお願いします。
【AGC015-D】A or ... or B problem を解いた
【自分の解法】
自明に$\ A\leq x\leq B\ $を満たす任意の$\ x \in \mathbb{N}\ $は構築できる。
ここで,伝家の宝刀†$\rm{dp}$†を用いて実験すると,どうやら$ A\leq x\leq l,\ r\leq x\leq f(A, B)\ $を満たす任意の$\ x \in \mathbb{N}\ $と構築できる$\ x \in \mathbb{N}\ $の集合が一致するような$l,\ r\ (l \leq r)$が存在するらしい。(ただし,$\ f(A,\ B)\ $は構築できる最大の整数)
このとき,求める答えは$$f(A,\ B) - A + 1 - max(r - l - 1, 0)$$である。
よって,この問題に解答する為には,$f(A,\ B),\ l,\ r$を求めればよい。
【$f(A, \ B)$を求める】
自明に$f(A, \ B) = A or ... or B$であるので,桁ごとに考える。
2進数で見て,$A,\ B$が上からみて下から$k$桁目まで一致しているとき,$k - 1$桁以下の桁は全て$1$にすることが可能なので,求める答えは,
$$ 2^k - 1 + \displaystyle \sum_{p = k}^{10^{1000}} (2^p\ \rm{and} \ B)$$
【$l,\ r$を求める】
まず,$A\leq \displaystyle \sum_{p = k}^{10^{1000}} (2^p\ \rm{and} \ B) \leq B$を満たすもののうち,最大のものを$v$とする。また,$B \leq l \leq r$であるので,
$$l = f(v, B),\ r = v\ \rm{or} \ A$$である。
これより,$B$の桁数を$N$として,時間計算量$\rm{O}(N)$でこの問題を解くことができた。
ABC167E-Colorful BlocksをDPで解きたかった話
問題概要
一列に$N$個のブロックが置いてある。それぞれのブロックを色$1$~$ M $のいずれかで塗るとき,隣接かつ同色なブロックの組が$K$個以下になるような塗り方の総数を$mod998244353$で求めよ。
コンテスト中
数え上げが苦手すぎて$O(N^2 M^2)$の$dp$が浮かんだ瞬間に飛ばしてFに行きました。(ちなみにFは結局解けずに冷えました。)
動的計画法で解きたい
まず,問題文を読むと次のような$dp$が浮かびます。
$dp[x][y][z]:=$先頭$x$個のブロックを隣接かつ同色な組が$y$組になるように,$x$個目のブロックを色$z$で塗るような塗り方の総数
このとき,遷移は
\begin{eqnarray} dp[x][y][z] = \begin{cases} 1 & ( x = 1 かつ y = 0 ) \\ dp[x-1][y-1][z] - dp[x-1][y][z] + \displaystyle \sum_{w=1}^{M} dp[x-1][y][w] & ( x > 1 かつ x > y ) \\ 0 & (otherwise) \\ \end{cases} \end{eqnarray}
また,求める答えは,
$$\sum_{v=0}^{K} \sum_{w=1}^{M} dp[N][v][w]$$
∴この問題を空間計算量$O(N^2 M)$, 時間計算量$O(N^2 M^2)$で解くことが出来ました。

(配列のサイズと型を入力すると何MBか教えてくれるうし)
まぁ間に合う訳がないんですが...
頭を少しだけ働かせると色ごとに重みがない(等価)なことを思い出します。
つまり,色に関する情報は不要なんですね。したがって,次のような$dp$が成り立ちます。
$dp[x][y]:=$先頭$x$個のブロックを隣接かつ同色な組が$y$組になるように塗るような塗り方の総数
遷移は,
\begin{eqnarray} dp[x][y] = \begin{cases} M & ( x = 1 かつ y = 0 ) \\ dp[x-1][y-1] + (M - 1) dp[x-1][y] & ( x > 1 かつ x > y ) \\ 0 & (otherwise) \\ \end{cases} \end{eqnarray}
(真ん中の式の捕捉:いる?)
このとき,求める答えは
$$\sum_{y=0}^{K} dp[N][y]$$
時間,空間計算量ともに$O(N^2)$なのでまだ間に合いません。
ここで,以下の等式(本質)に気づきます。
$$dp[P][y] = dp[P-y][0] \times _{P-y}H_y$$
これは,$P$個のブロックを隣接かつ同色な組が$y$組できるように並べることは,隣接かつ同色な組を全て同一と見做して$P-y$個のブロックを並べ,あとからどの$y$個のブロックを(重複を許して)複製するかを考えても同じなので成立します。
さて,上記の$dp$で求めたいものは
$$\sum_{y=0}^{K} dp[N][y]$$
でした。つまり,$dp[N][y]$の値が分かればよいのですが,上記の等式より,$dp[x][0]$の値が分かれば$dp[N][y]$の値が分かるので,結局,次のような$dp$になります。
$dp[x]:=$先頭$x$個のブロックを隣接かつ同色な組がないように塗るような塗り方の総数
遷移は,
\begin{eqnarray} dp[x][y] = \begin{cases} M & (x = 1) \\ (M - 1) dp[x-1] & ( x > 1) \\ \end{cases} \end{eqnarray}
求める答えは
$$\sum_{y=0}^{K} dp[N-y] \times _{N-y}H_y$$
$$= \sum_{y=0}^{K} M(M - 1)^{N-y-1} \times _{N-y+y-1}C_y$$
$$= M \sum_{y=0}^{K} (M - 1)^{N-y-1} \times _{N-1}C_y$$
これで,時間,空間計算量ともに$O(N)$で解くことが出来ました。
結局,直接数え上げるのとコードは同じになるのですが,こういうアプローチもあるよ~程度に紹介したかったので,しました。(雑に書いた部分はいつかちゃんと書きます。)